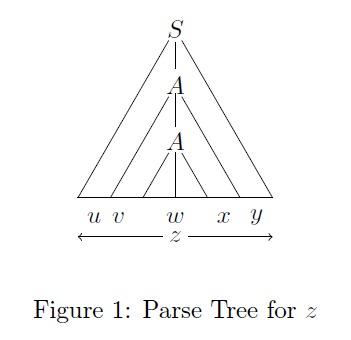
假設$L \subseteq \Sigma^*$是正則語言,存在字符串$w \in L$且$\left| w \right| \ge n$(n為泵長度,可理解為正則語言等效的有限自動機DFA狀態個數),如果可以將$w$寫成$w = uvxyz$的形式時,以下說法成立:
[用心去感覺] 哪些語言是上下文無關?
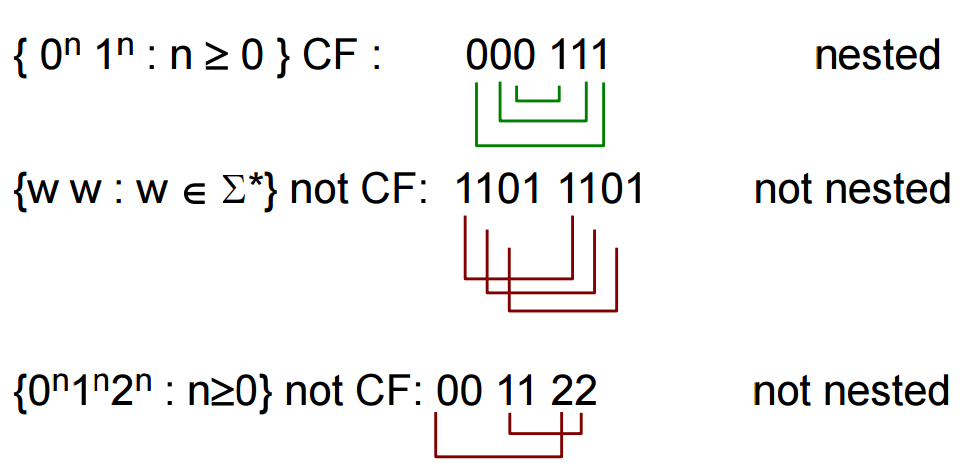
如果一個語言$L$的一部分是正則(regular)且有巢狀匹配,則感覺上應該是上下文無關(context-free)語言,如果沒有這種結構基本上都不是。
[例題] 三組符號 - Showing that $\{a^nb^nc^n: n ≥ 0\}$ is not a CFL
- 假設$a^Nb^Nc^N$屬於$L$語言的字串且比$N$長
($N$就是狀態個數,一個機器給$N$個狀態,要想辦法找到字串比$N$更長來達到重複的鴿籠效果) - 所以可以把$w$寫成$w = uvxyz$的形式($\left| vxy \right| \le n$, $\left| vy \right| > 0$)
- 而我們能證明存在$i$使$uv^ixy^iz$不在語言L中
分成兩個情況討論 :
- $vy$包含全部符號$a,b,c$,那麼$uv^ixy^iz$時$a,b,c$的順序會錯,例如 $(aa)(aaabb)(bb)(bccc)(cc)$變成$(aa)(aaabb)(aaabb)(bb)(bccc)(bccc)(cc)$,因此不在L中。
- $vy$不包含全部符號時,$uv^ixy^iz$會有不相同數量的a,b,c,例如$ (aa)(aaa)(bbbbb)(ccc)(cc)$變成$(aa)(aaa)(aaa)(bbbbb)(ccc)(ccc)(cc)$,因此不在L中。
[例題] 重複ww - Showing that $E = \{ww\ |\ w \in \{0,1\}^*\}$ is not a CFL
Proof. Suppose E is context-free. Let p be the pumping length.
Proof. Suppose E is context-free. Let p be the pumping length.
- Consider $z = 0^p1^p0^p1^p \in L$.
- Since $|z| > p$, there are $u, v, w, x, y$ such that $z = uvwxy, |vwx| ≤ p, |vx| > 0$ and $uv^iwx^iy \in L$ for all $i ≥ 0$.
- $vwx$ must straddle the midpoint of $z$.
- – Suppose $vwx$ is only in the first half. Then in $uv^2wx^2y$ the second half starts with 1. Thus, it is not of the form $ww$.
- – Case when $vwx$ is only in the second half. Then in $uv^2wx^2y$ the first half ends in a 0. Thus, it is not of the form $ww$.
- – Suppose $vwx$ straddles the middle. Then $uv^0wx^0y$ must be of the form $0^p1^i0^j1^p$, where either $i$ or $j$ is not $p$. Thus, $uv^0wx^0y \notin E$.
[例題] Same number of 0s and 1s
1. Showing that L = {w | w has the same number of 0s and 1s} is a CFL
Grammar G :
A → 0A1A | 1A0A
A → ε
2. Showing that B = {w|w is a palindrome over {0, 1} and w contains an equal number of 0s and 1s}
Reference
交大陳穎平教授正規語言講義
wiki - Pumping lemma for context-free languages
http://en.wikipedia.org/wiki/Pumping_lemma_for_context-free_languages
















沒有留言:
張貼留言