本篇不是介紹類神經網路和激勵函數是什麼,而是嘗試添加一些類神經網路設計思維上的血肉,讓整體思路更具體一點:會簡單介紹使用激勵函數的目的,以及如何選擇激勵函數。那就廢話不多說開始整理筆記吧^^
一、使用激勵函數的目的
懶人包:激勵函數主要作用是引入非線性。
在類神經網路中如果不使用激勵函數,那麼在類神經網路中皆是以上層輸入的線性組合作為這一層的輸出(也就是矩陣相乘),輸出和輸入依然脫離不了線性關係,做深度類神經網路便失去意義。
二、激勵函數的選擇:為何 ReLU 勝出?
懶人包:常見的激勵函數選擇有 sigmoid, tanh, Relu,實用上最常使用 ReLU ,一些變形如 Leaky ReLU, Maxout 也可以試試,tanh 和 sigmoid 盡量別用。
截至目前為止,在深度學習領域 Relu 激勵函數蔚為主流,主要考量的因素有以下幾點:
1. 梯度消失問題 (vanishing gradient problem)
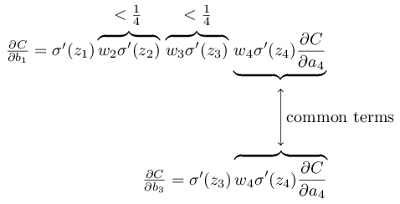
對使用反向傳播訓練的類神經網絡來說,梯度的問題是最重要的,使用 sigmoid 和 tanh 函數容易發生梯度消失問題,是類神經網絡加深時主要的訓練障礙。
具體的原因是這兩者函數在接近飽和區 (如sigmoid函數在 [-4, +4] 之外),求導後趨近於0,也就是所謂梯度消失,造成更新的訊息無法藉由反向傳播傳遞。
詳見:Why are deep neural networks hard to train?
http://neuralnetworksanddeeplearning.com/chap5.html
2. 類神經網路的稀疏性(奧卡姆剃刀原則)
Relu會使部分神經元的輸出為0,可以讓神經網路變得稀疏,緩解過度擬合的問題。
但衍生出另一個問題是,如果把一個神經元停止後,就難以再次開啟(Dead ReLU Problem),因此又有 Leaky ReLU 類 (x<0時取一個微小值而非0), maxout (增加激勵函數專用隱藏層,有點暴力) 等方法,或使用 adagrad 等可以調節學習率的演算法。
3. 生物事實:全有全無律 (all or none law)
在神經生理方面,當刺激未達一定的強度時,神經元不會興奮,因此不會產生神經衝動。如果超過某個強度,才會引起神經衝動。Relu比較好的捕捉了這個生物神經元的特徵。
4. 計算量節省
[補充1] Universal approximation theorem
Universal approximation theorem:用一層隱藏層的神經網絡,若使用的激勵函數具有單調遞增、有上下界、非常數且連續的性質,則總是存在一個擁有有限N個神經元的單隱藏層神經網絡可以無限逼近這個連續函數(鮑萊耳可測函數)。
但這個定理沒有說在這個神經網路裡的參數要怎麼學,只知道隱藏層的寬度會隨著問題複雜度提升變得非常大,因此,增加網絡深度的原因正是為了可以用更少的參數量實現同樣的逼近。
[補充2] 無免費午餐定理 No Free Lunch Theorem
這可以回答激勵函數選擇上,或任意最佳化演算法設計上的問題;不可能有一個最好的最佳化演算法設計適合所有的任務。
References
What is the best multi-stage architecture for object recognition? Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009a)
Deep sparse rectifier neural networks Glorot, X., Bordes, A., and Bengio, Y. (2011b).
Maxout networks. Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a).
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Maxout Networks. Ian J. Goodfellow, David Warde-Farley, Mehdi Mirza, Aaron Courville, Yoshua Bengio
Cybenko., G. (1989) Approximations by superpositions of sigmoidal functions
聊一聊深度學習的 activation function
https://zhuanlan.zhihu.com/p/25110450
人工神經網路的原理與訓練
https://zhuanlan.zhihu.com/p/22561439
知乎:請問人工神經網絡中的activation function的作用具體是什麼?為什麼ReLu要好過於tanh和sigmoid function?
https://www.zhihu.com/question/29021768
Neural Networks and Deep Learning - A visual proof that neural nets can compute any function
http://neuralnetworksanddeeplearning.com/chap4.html
Neural Networks and Deep Learning - Why are deep neural networks hard to train?
http://neuralnetworksanddeeplearning.com/chap5.html#discussion_why